Solved

On June 16, 1997, Two Amateur Golfers Playing Together Hit

Question 24

Multiple Choice

On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) = . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​


A) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
B) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
C) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
D) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is . If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = E) Pr(hole-in-one ∩ hole-in-one) =
E) Pr(hole-in-one ∩ hole-in-one) = On June 16, 1997, two amateur golfers playing together hit back-to-back holes in one (Source: The Island Packet, June 19, 1997) . Suppose the probability of an amateur golfer getting a hole-in-one is 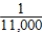. If the golfers' shots are independent of each other, what is the probability that two amateur golfers will get back-to-back holes in one? ​ A) Pr(hole-in-one ∩ hole-in-one) = B) Pr(hole-in-one ∩ hole-in-one) = 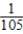C) Pr(hole-in-one ∩ hole-in-one) = D) Pr(hole-in-one ∩ hole-in-one) = 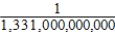E) Pr(hole-in-one ∩ hole-in-one) =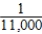

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q19: Suppose the following table summarizes the opinions

Q20: If a state wants each of its

Q21: The following table gives the numbers of

Q22: A fair die is rolled. Find the

Q23: From a deck of 52 playing cards,

Q25: Each of urns I and II has

Q26: An examination consists of 11 questions. If

Q27: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB1243/.jpg" alt="Find .

Q28: How many two-digit numbers can be formed

Q29: Three balls are drawn, without replacement, from