Suppose the Rate of Change of Total Personal Income I

Multiple Choice

Suppose the rate of change of total personal income I in the United States (in billions of dollars) can be modeled by 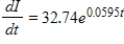, where t is the number of years past 1960. The value of are approximately $19,312.13 and $1,162.81 respectively which are been evaluated by using the arbitrary constant that is been evaluated by using the data point from 1960. Interpret 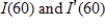. Round your answer to two decimal places, if necessary. ​

A)
Means that the model predicts that in 2020, the total personal income is predicted to be $19,312.13 billion dollars and will be decreasing at a rate of $1,162.81 billion per year.
B)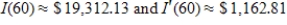
Means that the model predicts that in 2020, the total personal income is predicted to be $1,162.81 billion dollars and will be increasing at a rate of $19,312.13 billion per year.
C)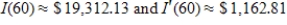
Means that the model predicts that in 2020, the total personal income is predicted to be $19,312.13 billion dollars and will be increasing at a rate of $1,162.81 billion per year.
D)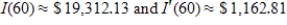
Means that the model predicts that in 2020, the total personal income is predicted to be $19,312.13 billion dollars and will be increasing at a rate of $1,162.81 billion per month.
E)
Means that the model predicts that in 2020, the total personal income is predicted to be $1,162.81 billion dollars and will be decreasing at a rate of $19,312.135 billion per month.