A Sports Analyst Was Interested in Finding Out How Well

Essay

A sports analyst was interested in finding out how well a football team's winning percentage (stated as a proportion) can be predicted based upon points scored and points allowed. She selects a random sample of 15 football teams. Each team played 10 games. She decided to use the point differential, points scored minus points allowed as the predictor variable. The data are shown in the table below, and regression output is given afterward.

$\begin{array}{|c|c|}\hline\text { Point Diff }&\text { Win Pct }\\\hline-75 & .100 \\\hline-60 & .300 \\\hline-40 & .200 \\\hline-33 & .300 \\\hline-21 & .400 \\\hline-15 & .500 \\\hline 5 & .500 \\\hline 14 & .700 \\\hline 20 & .600 \\\hline 28 & .700 \\\hline 31 & .800 \\\hline 45 & .900 \\\hline 56 & .700 \\\hline 72 & .600 \\\hline 80 & 1.000 \\\hline\end{array}$



$\text { Regression Analysis: Win Pct versus Point Diff }$
$\begin{array}{lrrrr}\text { Predictor } & \text { Coef } & \text { SE Coef } & \text { T } & \text { P } \\\text { Constant } & 0.51802 & 0.03071 & 16.87 & 0.000 \\\text { Point Diff } & 0.0049500 & 0.0006682 & 7.41 & 0.000\end{array}$
$S=0.117511 \quad \text { R-Sq }=80.8 \% \quad \text { R-Sq }(a d j)=79.48$
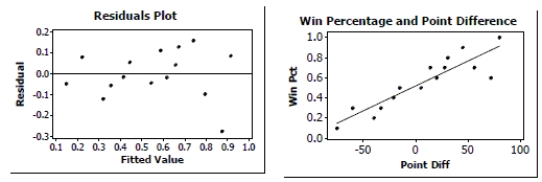
Is there evidence of an association between Point Differential and Winning Percentage? Test an appropriate hypothesis and state your conclusion in the proper context.