Multiple Choice
Use the graph to compute and . 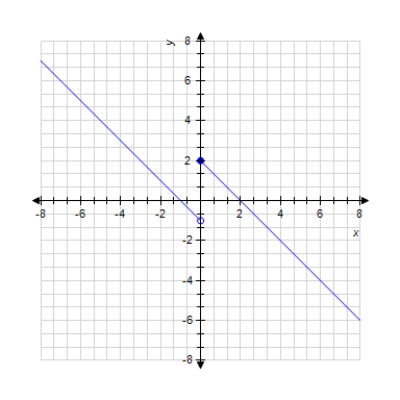
A) , .
B) , .
C) , .
D) , .
E) does not exist
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q28: Use a graph to determine whether
Q29: Calculate the average rate of change
Q30: Compute the derivative function <span
Q31: Determine what, if any, value to
Q32: Estimate <span class="ql-formula" data-value="f ^
Q34: Calculate the limit algebraically. <br>
Q35: Compute <span class="ql-formula" data-value="f ^
Q36: Draw the graph of a function that
Q37: Compute the derivative function <span
Q38: Compute <span class="ql-formula" data-value="f ^