In Each of the Following Cases, Decide Whether the Given $x ^ { t } \text { and } y ^ { t }$

Essay

In each of the following cases, decide whether the given function is intrinsically linear. If so, identify $x ^ { t } \text { and } y ^ { t }$ and then explain how a random error term $\varepsilon$
can be introduced to yield an intrinsically linear probabilistic model.
a. $y = 1 / ( \alpha + \beta x )$
b. $y = 1 / \left( 1 + e ^ { \alpha+ \beta x } \right)$
c.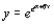
(a Gompertz curve)
d. $y = \alpha + \beta e ^ { \lambda x }$