Multiple Choice
The simple linear regression model is where
is a random variable assumed to be normally distributed with Let denote a particular value of the independent variable x. Which of the following identities are true regarding the expected or mean value of Y when ? 
A) 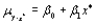
B) 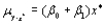
C) 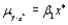
D) 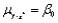
E) 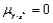
Correct Answer:

Verified
Correct Answer:
Verified
Q45: In a simple linear regression problem,
Q46: In testing <span class="ql-formula" data-value="H
Q47: The null hypothesis <span class="ql-formula"
Q48: In testing <span class="ql-formula" data-value="H
Q49: Which of the following statements are
Q51: Which of the following statements are
Q52: When the estimated regression line is
Q53: A study contains a plot of
Q54: Which of the following statements are
Q55: If <span class="ql-formula" data-value="\sum x