A Statistics Professor Investigated Some of the Factors That Affect $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$

Essay

A statistics professor investigated some of the factors that affect an individual student's final grade in his or her course. He proposed the multiple regression model: $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ .
Where:
y = final mark (out of 100). $x _ { 1 }$ = number of lectures skipped. $x _ { 2 }$ = number of late assignments. $X _ { 3 }$ = mid-term test mark (out of 100).
The professor recorded the data for 50 randomly selected students. The computer output is shown below.
THE REGRESSION EQUATION IS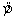
= $$41.6 - 3.18 x _ { 1 } - 1.17 x _ { 2 } + .63 x _ { 3 }$$ $$\begin{array} { | c | c c c | } \hline \text { Predictor } & \text { Coef } & \text { StDev } & \text { T } \\\hline \text { Constant } & 41.6 & 17.8 & 2.337 \\x _ { 1 } & - 3.18 & 1.66 & - 1.916 \\x _ { 2 } & - 1.17 & 1.13 & - 1.035 \\x _ { 3 } & 0.63 & 0.13 & 4.846 \\\hline\end{array}$$ S = 13.74 R-Sq = 30.0%. $$\begin{array}{l}\text { ANALYSIS OF VARIANCE }\\\begin{array} { | l | c c c c | } \hline \text { Source of Variation } & \text { df } & \text { SS } & \text { MS } & \text { F } \\\hline \text { Regression } & 3 & 3716 & 1238.667 & 6.558 \\\text { Error } & 46 & 8688 & 188.870 & \\\hline \text { Total } & 49 & 12404 & & \\\hline\end{array}\end{array}$$ Interpret the coefficients $b _ { 1 }$ and $b _ { 3 }$ .