Solved

Find Two Positive Real Numbers Whose Product Is a Maximum

Question 20

Multiple Choice

Find two positive real numbers whose product is a maximum and whose sum of the first number and four times the second is 280.


A) Find two positive real numbers whose product is a maximum and whose sum of the first number and four times the second is 280. A) B) C) D) E)
B) Find two positive real numbers whose product is a maximum and whose sum of the first number and four times the second is 280. A) B) C) D) E)
C) Find two positive real numbers whose product is a maximum and whose sum of the first number and four times the second is 280. A) B) C) D) E)
D) Find two positive real numbers whose product is a maximum and whose sum of the first number and four times the second is 280. A) B) C) D) E)
E) Find two positive real numbers whose product is a maximum and whose sum of the first number and four times the second is 280. A) B) 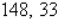C) 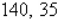D) 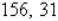E)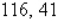

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q15: Write the quadratic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4588/.jpg" alt="Write

Q16: Use Descartes' Rule of Signs to determine

Q17: Use synthetic division to divide. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4588/.jpg"

Q18: Find all zeros of the function <img

Q19: Write the quadratic function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4588/.jpg" alt="Write

Q21: Find the standard form of the quadratic

Q22: Describe the right-hand and the left-hand behavior

Q23: An open box is to be made

Q24: Write the standard form of the equation

Q25: The height, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB4588/.jpg" alt="The height,