Solved

Find a Bound on the Error in Approximating the Given

Question 189

Multiple Choice

Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)


A) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)
B) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)
C) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) B) C) D)
D) Find a bound on the error in approximating the given definite integral using (a) the trapezoidal rule and (b) Simpson's rule with n intervals. A) 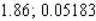B) 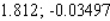C) 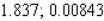D)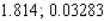

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q57: A university alumni group wishes to provide

Q184: Evaluate the following improper integral whenever it

Q185: Determine whether the given function is a

Q186: Evaluate the definite integral by using the

Q187: Evaluate the following improper integral whenever it

Q188: Evaluate the following improper integral whenever it

Q190: Use the table of integrals to find

Q191: Find the area of the region under

Q192: Find the area of the region bounded

Q193: The supply function for the CD manufactured