Solved

The Base Salary of a Salesman Working on Commission Is

Question 231

Multiple Choice

The base salary of a salesman working on commission is $13,000.For each $50,000 of sales beyond $100,000 he is paid a $1,000 commission.Sketch a graph showing his earnings as a function of the level of his sales x.


A) The base salary of a salesman working on commission is $13,000.For each $50,000 of sales beyond $100,000 he is paid a $1,000 commission.Sketch a graph showing his earnings as a function of the level of his sales x. A) B) C)
B) The base salary of a salesman working on commission is $13,000.For each $50,000 of sales beyond $100,000 he is paid a $1,000 commission.Sketch a graph showing his earnings as a function of the level of his sales x. A) B) C)
C) The base salary of a salesman working on commission is $13,000.For each $50,000 of sales beyond $100,000 he is paid a $1,000 commission.Sketch a graph showing his earnings as a function of the level of his sales x. A) 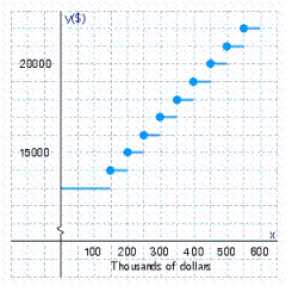B) 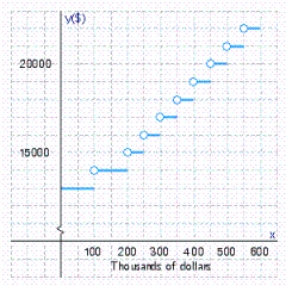C)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q226: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7866/.jpg" alt="Let .

Q227: Find the domain of the function <img

Q228: Find the one-sided limit, if it exists.If

Q229: Find the domain of the function. <img

Q230: Find the one-sided limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7866/.jpg" alt="Find

Q232: Complete the table by computing <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7866/.jpg"

Q233: Use the graph of the function f

Q234: Find the slope of the tangent line

Q235: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7866/.jpg" alt="Let Find

Q236: Find the indicated one-sided limit. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7866/.jpg"