In a Study of the Effects of Rewards on Learning

Essay

In a study of the effects of rewards on learning in rats, an experimenter divided 20 rats into 4 groups of equal sizes. Each rat was run through a maze, and there was only one correct method of exiting the maze. The rats were rewarded on different schedules. The investigators observed the number of trials it took the rats to learn the maze.
Group A: The rats were rewarded for every correct direction chosen in the maze
Group B: The rats were randomly rewarded 75% of the time
Group C: The rats were randomly rewarded 25% of the time
Group D: The rats were not rewarded at all.
The following table contains summary information for this experiment. ​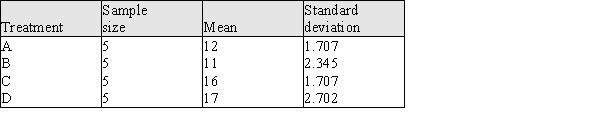
a) Construct the appropriate ANOVA table and test the hypothesis that there is no difference between the mean number of trials needed to learn the maze for the different reward treatments.
b) Is there evidence that the 25% random reward schedule and the 75% random reward schedule result in a different mean number of trials to learn the maze? Give statistical evidence to support your answer.