Hervis Car Rental in Austin, TX Has 50 High-Performance Shelby-H

Essay

Hervis Car Rental in Austin, TX has 50 high-performance Shelby-H Mustangs in its rental fleet. These cars will be in greater demand than usual during the last weekend in July when the Central Texas Mustang Club holds its annual rally in Austin. At times like this, Hervis uses a revenue management system to determine the optimal number of reservations to have available for the Shelby-H cars.
Hervis has agreed to have at least 60% of its Shelby-H Mustangs available for rally attendees at a special rate. Although many of the rally attendees will request a Saturday and Sunday two-day package, some attendees may select a Saturday only or a Sunday only reservation. Customers not attending the rally may also request a Saturday and Sunday two-day package, or make a Saturday only or Sunday only reservation. Thus, six types of reservations are possible. The cost for each type of reservation is shown here. The anticipated demand for each type of reservation is as follows: 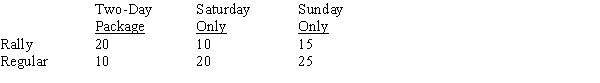Hervis Car Rental would like to determine how many Shelby-H Mustangs to make available for each type of reservation in order to maximize total revenue.
a.
Define the decision variables.
b.
Formulate a linear programming model for this revenue management application.