Creative Kitchen Tools Manufactures a Wide Line of Gourmet Cooking

Essay

Creative Kitchen Tools manufactures a wide line of gourmet cooking tools from stainless steel. For the coming production period, there is demand of 1200 for 8 quart stock pots, and unlimited demand for 3 quart mixing bowls and large slotted spoons. In the following model, the three variables measure the number of pots, bowls, and spoons to make. The objective function measures profit. Constraint 1 measures steel, constraint 2 measures manufacturing time, constraint 3 measures finishing time, and constraint 4 measures the stock pot demand.
Max
5x₁ + 3x₂ + 6x₃
s.t.
3x₁ + 1x₂ + 2x₃ ≤ 15000
4x₁ + 4x₂ + 5x₃ ≤ 18000
2x₁ + 1x₂ + 2x₃ ≤ 10000
x₁ ≤ 1200
x₁, x₂, x₃ ≥ 0
​
The final tableau is: ​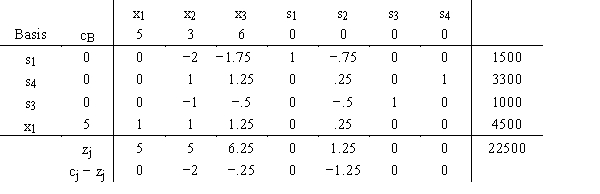
a.
Calculate the range of optimality for c₁, c₂, and c₃.
b.
Calculate the range of feasibility for b₁, b₂, b₃, and b₄.
c.
​
Suppose that the inventory records were incorrect and the company really has only 14000 units of steel. What effect will this have on your solution?
d.
​
Suppose that a cost increase will change the profit on the pots to $4.62. What effect will this have on your solution?
e.
​
​
Assume that the cost of time in production and finishing is relevant. Would you be willing to pay a $1.00 premium over the normal cost for 1000 more hours in the production department? What would this do to your solution?