Solved

The Linear Programming Problem

Question 18

Essay

The linear programming problem:
Max
6x1 + 2x2 + 3x3 + 4x4
s.t.
x1 + x2 + x3 + x4 ≤ 100
4x1 + x2 + x3 + x4 ≤ 160
3x1 + x2 + 2x3 + 3x4 ≤ 240
x1, x2, x 3, x4 ≥ 0
​
has the final tableau: The linear programming problem: Max 6x<sub>1</sub> + 2x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> s.t. x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 100 4x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 160 3x<sub>1</sub> + x<sub>2</sub> + 2x<sub>3</sub> + 3x<sub>4</sub> ≤ 240 x<sub>1</sub>, x<sub>2</sub>, x <sub>3</sub>, x<sub>4</sub> ≥ 0 ​ has the final tableau: ​ Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem. LINEAR PROGRAMMING PROBLEM MAX 6X1+2X2+3X3+4X4 S.T. 1) 1X1 + 1X2 + 1X3 + 1X4 < 100 2) 4X1 + 1X2 + 1X3 + 1X4 < 160 3) 3X1 + 1X2 + 2X3 + 3X4 < 240 ​ OPTIMAL SOLUTION Objective Function Value = ​ ​ OBJECTIVE COEFFICIENT RANGES ​ RIGHT HAND SIDE RANGES ​
Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem.
LINEAR PROGRAMMING PROBLEM
MAX
6X1+2X2+3X3+4X4
S.T.
1) 1X1 + 1X2 + 1X3 + 1X4 < 100
2) 4X1 + 1X2 + 1X3 + 1X4 < 160
3) 3X1 + 1X2 + 2X3 + 3X4 < 240
​
OPTIMAL SOLUTION
Objective Function Value = The linear programming problem: Max 6x<sub>1</sub> + 2x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> s.t. x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 100 4x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 160 3x<sub>1</sub> + x<sub>2</sub> + 2x<sub>3</sub> + 3x<sub>4</sub> ≤ 240 x<sub>1</sub>, x<sub>2</sub>, x <sub>3</sub>, x<sub>4</sub> ≥ 0 ​ has the final tableau: ​ Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem. LINEAR PROGRAMMING PROBLEM MAX 6X1+2X2+3X3+4X4 S.T. 1) 1X1 + 1X2 + 1X3 + 1X4 < 100 2) 4X1 + 1X2 + 1X3 + 1X4 < 160 3) 3X1 + 1X2 + 2X3 + 3X4 < 240 ​ OPTIMAL SOLUTION Objective Function Value = ​ ​ OBJECTIVE COEFFICIENT RANGES ​ RIGHT HAND SIDE RANGES ​ The linear programming problem: Max 6x<sub>1</sub> + 2x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> s.t. x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 100 4x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 160 3x<sub>1</sub> + x<sub>2</sub> + 2x<sub>3</sub> + 3x<sub>4</sub> ≤ 240 x<sub>1</sub>, x<sub>2</sub>, x <sub>3</sub>, x<sub>4</sub> ≥ 0 ​ has the final tableau: ​ Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem. LINEAR PROGRAMMING PROBLEM MAX 6X1+2X2+3X3+4X4 S.T. 1) 1X1 + 1X2 + 1X3 + 1X4 < 100 2) 4X1 + 1X2 + 1X3 + 1X4 < 160 3) 3X1 + 1X2 + 2X3 + 3X4 < 240 ​ OPTIMAL SOLUTION Objective Function Value = ​ ​ OBJECTIVE COEFFICIENT RANGES ​ RIGHT HAND SIDE RANGES ​
OBJECTIVE COEFFICIENT RANGES The linear programming problem: Max 6x<sub>1</sub> + 2x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> s.t. x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 100 4x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 160 3x<sub>1</sub> + x<sub>2</sub> + 2x<sub>3</sub> + 3x<sub>4</sub> ≤ 240 x<sub>1</sub>, x<sub>2</sub>, x <sub>3</sub>, x<sub>4</sub> ≥ 0 ​ has the final tableau: ​ Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem. LINEAR PROGRAMMING PROBLEM MAX 6X1+2X2+3X3+4X4 S.T. 1) 1X1 + 1X2 + 1X3 + 1X4 < 100 2) 4X1 + 1X2 + 1X3 + 1X4 < 160 3) 3X1 + 1X2 + 2X3 + 3X4 < 240 ​ OPTIMAL SOLUTION Objective Function Value = ​ ​ OBJECTIVE COEFFICIENT RANGES ​ RIGHT HAND SIDE RANGES ​
RIGHT HAND SIDE RANGES The linear programming problem: Max 6x<sub>1</sub> + 2x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> s.t. x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 100 4x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> + x<sub>4</sub> ≤ 160 3x<sub>1</sub> + x<sub>2</sub> + 2x<sub>3</sub> + 3x<sub>4</sub> ≤ 240 x<sub>1</sub>, x<sub>2</sub>, x <sub>3</sub>, x<sub>4</sub> ≥ 0 ​ has the final tableau: ​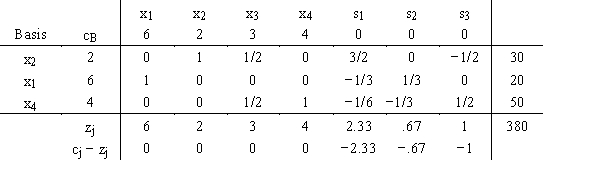 Fill in the table below to show what you would have found if you had used The Management Scientist to solve this problem. LINEAR PROGRAMMING PROBLEM MAX 6X1+2X2+3X3+4X4 S.T. 1) 1X1 + 1X2 + 1X3 + 1X4 < 100 2) 4X1 + 1X2 + 1X3 + 1X4 < 160 3) 3X1 + 1X2 + 2X3 + 3X4 < 240 ​ OPTIMAL SOLUTION Objective Function Value = ​ ​ OBJECTIVE COEFFICIENT RANGES ​ RIGHT HAND SIDE RANGES

Correct Answer:

verifed

Verified

LINEAR PROGRAMMING PROBLEM
MAX
6X1 + 2X2...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q8: The range of optimality is calculated by

Q13: If the dual price for b<sub>1</sub> is

Q14: The number of constraints to the dual

Q17: Given the following linear programming problem<br>Max<br>10x<sub>1</sub> +

Q19: The range of optimality is useful only

Q19: For this optimal simplex tableau the original

Q20: There is a dual price associated with

Q21: ​Explain why the zj value for a

Q22: The range of feasibility indicates right-hand side

Q23: ​When sensitivity calculations yield several potential upper