Multiple Choice
Given that and are non-zero vectors and that and , then which of the following MUST be true? Select all that apply.
A) is perpendicular to .
B) is parallel or anti-parallel to .
C) The angle between
and
satisfies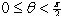 .
.
D) The angle between
and
satisfies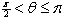 .
.
E) At least one of and
is greater than 1.
Correct Answer:

Verified
Correct Answer:
Verified
Q32: The vectors <span class="ql-formula" data-value="\vec
Q33: Let <span class="ql-formula" data-value="\vec {
Q34: Let <span class="ql-formula" data-value="\vec {
Q35: The plane <span class="ql-formula" data-value="x
Q36: The triangle ABC with vertices
Q38: Determine the distance from the plane
Q39: For what value(s)of a is the
Q40: Consider the plane <span class="ql-formula"
Q41: If <span class="ql-formula" data-value="\vec {
Q42: If <span class="ql-formula" data-value="\vec {