Cesium 137 (Cs¹³⁷)is a Short-Lived Radioactive Isotope $e^{-\left(\frac{\ln 2}{30}\right) t}$

Short Answer

Cesium 137 (Cs¹³⁷)is a short-lived radioactive isotope.It decays at a rate proportional to the amount of itself present and has a half-life of 30 years (i.e., the amount of Cs¹³⁷ remaining t years after A₀ mg of the radioactive isotope is released is given by 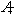$e^{-\left(\frac{\ln 2}{30}\right) t}$ ).As a result of its operations, a nuclear power plant releases Cs¹³⁷ at a rate of 0.1 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.In the long run, approximately how many mg of Cs¹³⁷ will there be? Round to 2 decimal places.