Consider the Following Two Games

Not Answered

Consider the following two games:
Game 1: There are 10 balls of different colors, you pick one of the proposed balls. After you have made your choice and have put the ball back, one ball is selected at random. If the selected ball matches the ball you picked, you win.
Game 2: There are 6 balls of different colors, you pick two of the proposed balls. After you have made your choices and have put balls back, two different balls are selected at random. If the selected balls match the two you picked, you win.
If you can only play one of these games, which game would you pick to win and why? Use relevant probabilities to justify your choice.
A)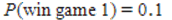 and , therefore it is advantageous to play game 1 because the probability of winning is higher.
B)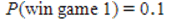 and , therefore it is advantageous to play game 2 because the probability of winning is higher.
C)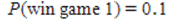 and P(win game 2) = 0.033, therefore it is advantageous to play game 1 because the probability of winning is higher.
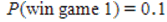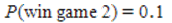D) and , therefore it is no matter what game to play because the probabilities of winning are equal.
E)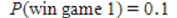 and , therefore it is advantageous to play game 2 because the probability of winning is higher.