Solved

When Testing Hypotheses About and Constructing Confidence Intervals for μ1

Question 16

Essay

When testing hypotheses about and constructing confidence intervals for μ1 − μ2, we utilize the statistic, When testing hypotheses about and constructing confidence intervals for μ<sub>1</sub> − μ<sub>2</sub>, we utilize the statistic, . What are the mean and standard deviation of the sampling distribution of ? . What are the mean and standard deviation of the sampling distribution of When testing hypotheses about and constructing confidence intervals for μ<sub>1</sub> − μ<sub>2</sub>, we utilize the statistic, 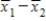. What are the mean and standard deviation of the sampling distribution of ? ?

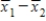Correct Answer:

verifed

Verified

The mean of the samp...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q11: In a recent paper, the authors distinguish

Q12: A recent paper described an experiment in

Q13: A common memory task is the classification

Q14: Researchers have hypothesized that female Downy Woodpeckers

Q15: The home range of an animal is

Q17: A researcher investigates the effect of a

Q18: For two independent samples, <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB7677/.jpg" alt="For

Q19: As part of the iguana risk assessment

Q20: An article describes a study of the

Q21: A common memory task is the classification