Solved

Suppose 8 Adult Patients with the Same Diagnosis Were Randomly

Question 42

Multiple Choice

Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. 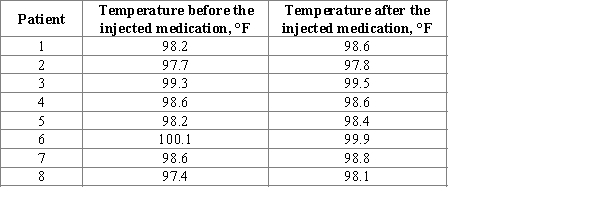Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication. A) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021. B) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​ C) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023. D) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​ E) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication.


A) The confidence interval is
Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication. A) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021. B) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​ C) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023. D) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​ E) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131. .
You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021.
B) The confidence interval is
Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication. A) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021. B) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​ C) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023. D) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​ E) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131. .
You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​
C) The confidence interval is
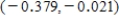Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication. A) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021. B) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​ C) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023. D) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​ E) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131. .
You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023.
D) The confidence interval is
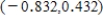Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication. A) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021. B) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​ C) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023. D) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​ E) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131. .
You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​
E) The confidence interval is
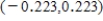Suppose 8 adult patients with the same diagnosis were randomly selected. Researchers want to check whether the injected medication will affect the change in body temperature. The patient's body temperature was measured before and after the injected medication and resulting data are given in the accompanying table. ​ Construct and interpret a 95% confidence interval estimate for the difference in mean temperature before and after the injected medication. A) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.379 and -0.021. B) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.832 and 0.432.​ C) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.423 and 0.023. D) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.223 and 0.223.​ E) The confidence interval is . You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131. .
You can be 95% confident that the actual difference in mean temperature before and after the injected medication for adult patients with this diagnosis is between -0.531 and 0.131.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q36: As part of the foraging behavior assessment

Q37: Suppose a researcher is testing a new

Q38: Does the gas leakage rate from automobile

Q39: In 1992 Hurricane Andrew struck Florida causing

Q40: Body fat and lean body mass can

Q41: The data below give the weights in

Q43: The researchers suggested that the time of

Q44: Researchers assessed the effectiveness of courses on

Q45: When creating a confidence interval involving treatment

Q46: Samples from two independent, normally-distributed populations produced