Suppose 9 Adult Smokers Were Randomly Selected

Multiple Choice

Suppose 9 adult smokers were randomly selected. Researchers want to check whether the movie about the dangers of smoking affects the number of cigarettes smoked. The number of cigarettes per day before and after watching the movie was recorded for each smoker from the sample and resulting data are given in the accompanying table. ​ Select the most appropriate 95% bootstrap confidence interval for a difference in the mean number of cigarettes per day before and after watching the movie for adult smokers and its correct interpretation.

A) The bootstrap confidence interval is 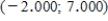.You can be 95% confident that the actual difference in mean number of cigarettes per day before and after watching the movie is between -2.000 and 7.000.
B) The bootstrap confidence interval is 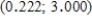.You can be 95% confident that the actual difference in mean number of cigarettes per day before and after watching the movie is between 0.222 and 3.000.
C) The bootstrap confidence interval is 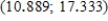.You can be 95% confident that the actual difference in mean number of cigarettes per day before and after watching the movie is between 10.889 and 17.333.
D) The bootstrap confidence interval is 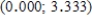.You can be 95% confident that the actual difference in mean number of cigarettes per day before and after watching the movie is between 0.000 and 3.333.
E) The bootstrap confidence interval is 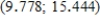.You can be 95% confident that the actual difference in mean number of cigarettes per day before and after watching the movie is between 9.778 and 15.444.