Multiple Choice
Researchers studied how many steps a day adult residents of the city make. They determined that the mean number of steps per day for a representative sample of 10 adult residents of the city was 5,139 steps. The original sample data values are:  Researchers are interested in deciding if there is evidence that adult residents of the city make more than 5,000 steps per day. Use a randomization test to select the appropriate output for one set of 1,000 simulated sample means and carry out a hypothesis test for a population mean.
Researchers are interested in deciding if there is evidence that adult residents of the city make more than 5,000 steps per day. Use a randomization test to select the appropriate output for one set of 1,000 simulated sample means and carry out a hypothesis test for a population mean.
A) 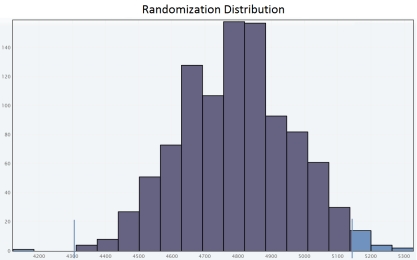
 Since the approximate P-value is less than
Since the approximate P-value is less than 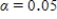 , we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
B) 
 Since the approximate P-value is greater than
Since the approximate P-value is greater than  , we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
C) 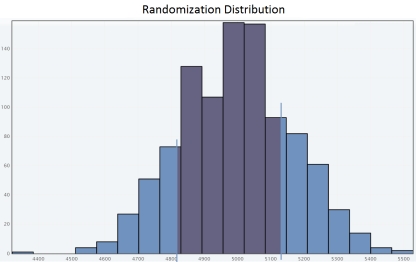

Since the approximate P-value is greater than 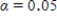 , we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
D) 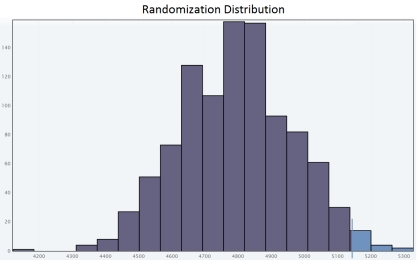

Since the approximate P-value is less than 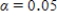 , we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we reject H0 for a significance level of 0.05.So the sample provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
E) 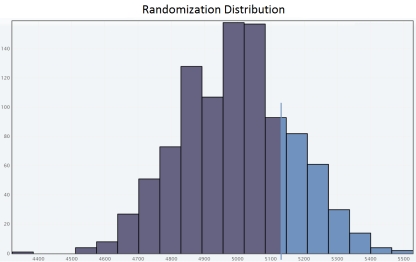

Since the approximate P-value is greater than 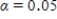 , we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
, we fail to reject H0 for a significance level of 0.05.So the sample does not provide convincing evidence that adult residents of the city make more than 5,000 steps per day.
Correct Answer:

Verified
Correct Answer:
Verified
Q27: A company provides portable walkie-talkies to construction
Q36: The Environmental Protection Agency (EPA) is charged
Q41: A recent survey sampled 1,086 parents of
Q42: A boat manufacturer claims that a particular
Q43: Researchers conducted a survey among 1793 families
Q44: A random sample of the houses in
Q45: The spread of the sample mean decreases
Q46: A report states that the mean yearly
Q48: Under what conditions is the z confidence
Q50: A packaging machine is supposed to fill