Multiple Choice
Graph the function by making a table of coordinates
- 
A) 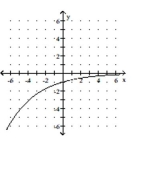
B) 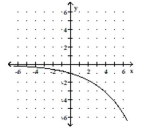
C) 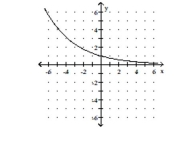
D) 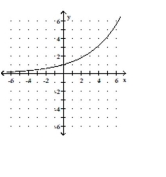
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q123: Use properties of logarithms to expand
Q124: Use properties of logarithms to expand
Q125: Graph the function.<br>-Use the graph of
Q126: Write the equation in its equivalent
Q127: Evaluate the expression without using a
Q129: Graph the function.<br>-Use the graph of
Q130: Graph the function.<br>-Use the graph of
Q131: Write the equation in its equivalent
Q132: Evaluate or simplify the expression without
Q133: Graph the function.<br>-Use the graph of