Multiple Choice
Graph the function.
-Use the graph of to obtain the graph of .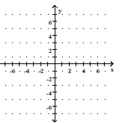
A) 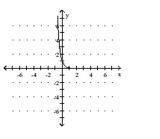
B) 
C) 
D) 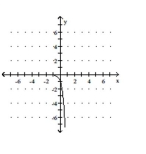
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q60: Evaluate the expression without using a
Q61: Evaluate the expression without using a
Q62: Solve the problem.<br>-Use the formula
Q63: <span class="ql-formula" data-value="\text { Use the compound
Q64: <span class="ql-formula" data-value="\text { Use the compound
Q66: Graph the function.<br>-Use the graph of
Q67: Find the domain of the logarithmic
Q68: Use properties of logarithms to expand
Q69: <span class="ql-formula" data-value="\text { Use the compound
Q70: Evaluate the expression without using a