Multiple Choice
Graph the function.
-Use the graph of to obtain the graph of .
A) 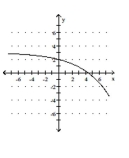
B) 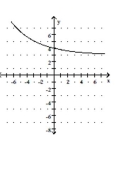
C) 
D) 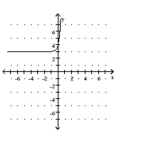
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q46: Graph the functions in the same
Q47: Graph the function.<br>-Use the graph of
Q48: Write the equation in its equivalent
Q49: Use properties of logarithms to expand
Q50: Approximate the number using a calculator.
Q52: Solve the problem.<br>-The population in a
Q53: Solve the problem.<br>-The long jump record, in
Q54: Graph the function by making a
Q55: Graph the function.<br>-Use the graph of
Q56: Use properties of logarithms to expand