Multiple Choice
Graph the function.
-Use the graph of to obtain the graph of .
A) 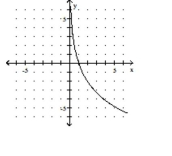
B) 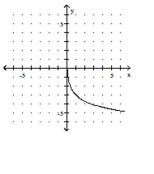
C) 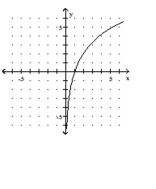
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q30: Find the domain of the logarithmic
Q31: Graph the function.<br>-Use the graph of
Q32: Use properties of logarithms to expand
Q33: Evaluate the expression without using a
Q34: Use properties of logarithms to expand
Q36: Write the equation in its equivalent
Q37: Approximate the number using a calculator.
Q38: Solve the problem.<br>-The <span class="ql-formula"
Q39: Use properties of logarithms to expand
Q40: Evaluate the expression without using a