Multiple Choice
Determine whether the function is one-to-one. If it is one-to-one find an equation or a set of ordered pairs that defines
the inverse function of the given function.
-
A) 
B) 
C)
D) 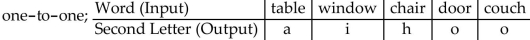
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q245: Determine whether the function is a
Q246: Express as the logarithm of a
Q247: The graph of an exponential function
Q248: Find the value of the logarithmic
Q249: Use the exponential decay formula with
Q251: Write as an exponential equation.<br>- <span
Q252: Solve the equation.<br>- <span class="ql-formula" data-value="\log
Q253: Determine whether the functions f and
Q254: Graph the function and its inverse
Q255: Solve.<br>-Hector borrows $3750 at a rate