Solved

Match the Polynomial Function with Its Graph f(x)=x(x−1)(x+1)f ( x ) = x ( x - 1 ) ( x + 1 )

Question 65

Multiple Choice

Match the polynomial function with its graph.
- f(x) =x(x−1) (x+1) f ( x ) = x ( x - 1 ) ( x + 1 )


A)
Match the polynomial function with its graph. - f ( x ) = x ( x - 1 ) ( x + 1 ) A) B) C) D)
B)
Match the polynomial function with its graph. - f ( x ) = x ( x - 1 ) ( x + 1 ) A) B) C) D)
C)
Match the polynomial function with its graph. - f ( x ) = x ( x - 1 ) ( x + 1 ) A) B) C) D)
D)
Match the polynomial function with its graph. - f ( x ) = x ( x - 1 ) ( x + 1 ) A) 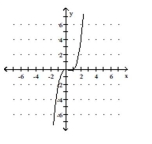B) 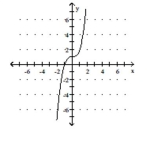C) 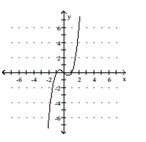D)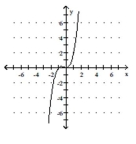

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q60: Fill in the blank with one of

Q61: Divide.<br>- <span class="ql-formula" data-value="\left( x ^

Q62: Fill in the blank with one of

Q63: Use substitution to factor the polynomial

Q64: Factor the polynomial.<br>- <span class="ql-formula" data-value="x

Q66: Factor the polynomial completely.<br>- <span class="ql-formula"

Q67: Multiply.<br>- <span class="ql-formula" data-value="( x -

Q68: Divide.<br>- <span class="ql-formula" data-value="\left( 2 x

Q69: Fill in the blank with one of

Q70: Multiply. Assume that variables used as