Multiple Choice
Sketch the graph of the equation. If the graph is a parabola, find its vertex. If the graph is a circle, find its center andradius.
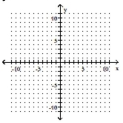
A) 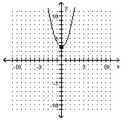
B) 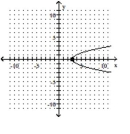
C) 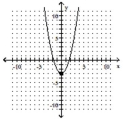
D) 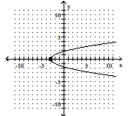
Correct Answer:

Verified
Correct Answer:
Verified
Q2: Find the center and the radius
Q3: Graph the system.<br>- <span class="ql-formula" data-value="\left\{
Q4: Graph the inequality.<br>- <span class="ql-formula" data-value="y
Q5: Graph the equation.<br>- <span class="ql-formula" data-value="\frac
Q6: Graph the equation.<br>- <span class="ql-formula" data-value="y=x^{2}-8
Q8: Solve the system.<br>- <span class="ql-formula" data-value="\left\{
Q9: Sketch the graph of the equation.
Q10: Graph the inequality.<br>- <span class="ql-formula" data-value="y>-x^{2}"><span
Q11: Graph the equation.<br>- <span class="ql-formula" data-value="\frac
Q12: Graph the equation.<br>- <span class="ql-formula" data-value="x^{2}-4