Multiple Choice
Graph the function and write the domain and range in interval notation.
-
A) 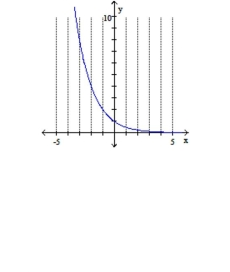
Domain:
Range:
B) 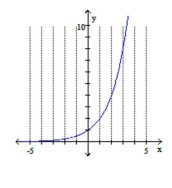
Domain:
Range:
C) 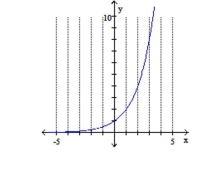
Domain:
Range:
D) 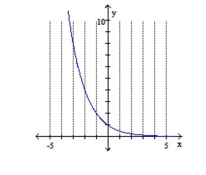
Domain:
Range:
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q93: Write as the sum or difference
Q94: Write the logarithmic expression as a
Q95: Solve the equation. Write the solution
Q96: Write the logarithm as a sum
Q97: Approximate the value of the logarithm
Q99: Graph the function.<br>- <span class="ql-formula" data-value="y
Q100: Solve the equation. Write the solution
Q101: Solve the problem.<br>-Use the graph of
Q102: Solve the problem.<br>-The enrollment at one
Q103: Simplify the expression without using a