Multiple Choice
a. Use transformations to graph the function.
b. Write the domain and range in interval notation.
c. Determine the vertical asymptote.
-
A) .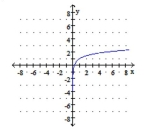
b. domain: , range
c. vertical asymptote:
B) .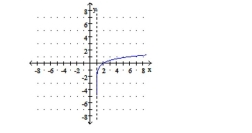
b. domain: , range
c. vertical asymptote:
C) .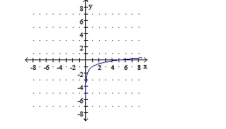
b. domain: , range
c. vertical asymptote:
D) .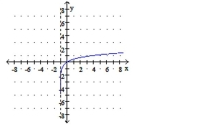
b. domain: , range
c. vertical asymptote:
Correct Answer:

Verified
Correct Answer:
Verified
Q77: Solve the problem.<br>-The limiting magnitude
Q78: Graph the function and write the
Q79: Find the inverse mentally.<br>- <span class="ql-formula"
Q80: Write the word or phrase that
Q81: Choose the one alternative that best
Q83: The graph of a function and its
Q84: Write the logarithm as a sum
Q85: Given f (x), write an equation
Q86: Write the word or phrase that
Q87: A one-to-one function is given. Write