Solve the Problem Monthly Cost (Jan $( \mathrm { t } = 0$

Multiple Choice

Solve the problem.
-The monthly costs for a small company to do business has been increasing over time in part due to inflation. The table gives the monthly cost y (in $) for the month of January for selected years. The Variable t represents the number of years since 2008.
$\begin{array}{c|c}\begin{array}{c}\text { Year } \\(t=\mathbf{0} \text { is 2008) }\end{array} & \begin{array}{c}\text { Monthly } \\\text { Costs (\$) } y\end{array} \\\hline 0 & 14,000 \\1 & 14,200 \\2 & 14,400 \\3 & 14,600\end{array}$

Monthly Cost (Jan.) for Selected Years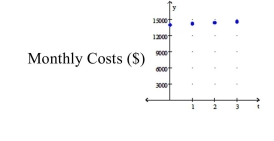



Year $( \mathrm { t } = 0$ represents $2008 )$

a. Use a graphing utility to find a model of the form $y = a b ^ { t }$ .
b. Write the function from part (a) as an exponential function with base $e$ .
c. Use the model to predict the monthly cost for January in the year 2,017 if this trend continues. Round to the nearest hundred dollars.

A) a. $y = 14,001 ( 0.0140 ) ^ { t }$
b. $y = 10 e ^ { 0.0140 t }$
c. $\$ 91,900$

B) a. $y = 14,001 ( 1.014 ) ^ { t }$
b. $y = 14,001 e ^ { 0.0140 t }$
c. $\$ 15,900$

C) a. $y = 14,001 ( 1.014 ) ^ { t }$
b. $y = 10 e ^ { 0.0140 t }$
c. $\$ 15,900$

D) a. $y = 14,001 ( 1.014 ) ^ { t }$
b. $y = 10 e ^ { 1.014 t }$
c. $\$ 91,900$