Determine If the Graph Can Represent a Polynomial Function $- 2,1$

Multiple Choice

Determine if the graph can represent a polynomial function. If so, assume the end behavior and all turning points are represented on the graph.
-
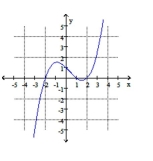
a. Determine the minimum degree of the polynomial based on the number of turning points.
b. Determine whether the leading coefficient is positive or negative based on the end behavior and Whether the degree of the polynomial is odd or even.
c. Approximate the real zeros of the function, and determine if their multiplicity is odd or even.

A) a. Minimum degree 3
b. Leading coefficient positive degree odd
c. $- 2,1$ , and 2 (each with odd multiplicity)
B) a. Minimum degree 3
b. Leading coefficient negative degree odd
c. $- 2$ (odd multiplicity) , 1 (even multiplicity) , 2 (even multiplicity)
C) a. Minimum degree 2
b. Leading coefficient negative degree even
c. $- 2$ (odd multiplicity) , 1 (even multiplicity) , 2 (even multiplicity)
D) Not a polynomial function.