Solve the Problem $$f ( x ) = - \frac { 1 } { 8 } ( x - 1 ) ^ { 4 }$$

Multiple Choice

Solve the problem.
- $$f ( x ) = - \frac { 1 } { 8 } ( x - 1 ) ^ { 4 }$$
a. Identify the power function of the form $y = x ^ { n }$ that is the parent function to the given graph.
b. In order, outline the transformations that would be required on the graph of $y = x ^ { n }$ to make the graph of the given function.
c. Match the function with the graph.
i.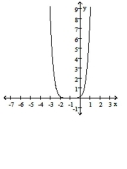


ii.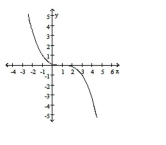


iii.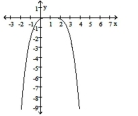


iv.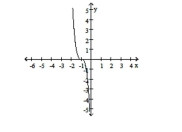

A) a. $y = x ^ { 4 }$
b. Shift $y = x ^ { 4 }$ to the right 1 units. Shrink vertically by a factor of $\frac { 1 } { 8 }$ . Reflect across the $x$ -axis.
c. Graph iii.
B) a. $y = x ^ { 4 }$
b. Shift $y = x ^ { 4 }$ to the left 1 units. Shrink vertically by a factor of $\frac { 1 } { 4 }$ . Reflect across the $x$ -axis.
c. Graph iii.
C) a. $y = x ^ { 4 }$
b. Shift $y = x ^ { 4 }$ to the right 1 units. Shrink vertically by a factor of $\frac { 1 } { 8 }$ . Reflect across the $x$ -axis.
c. Graph ii.
D) a. $y = x ^ { 4 }$
b. Shift $y = x ^ { 4 }$ to the left 1 units. Shrink vertically by a factor of $\frac { 1 } { 4 }$ .
c. Graph i.