Multiple Choice
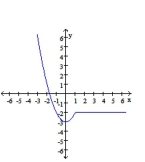
Produce a rule for the function whose graph is shown.
-
A)
B)
C)
D)
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q197: Determine whether the relation defines y as
Q198: Write the domain in interval notation.<br>-
Q199: Use the given information about a
Q200: The graphs of f and g
Q201: Evaluate the function for the given
Q203: Solve the problem.<br>-Joey borrows $2,400 from his
Q204: Write the domain in interval notation.<br>-
Q205: Determine the average rate of change
Q206: Evaluate the function for the indicated
Q207: Solve the problem.<br>-The following figure represents