Solve the Problem $A = \pi r \sqrt { r ^ { 2 } + h ^ { 2 } }$

Multiple Choice

Solve the problem.
-The lateral surface area A of a right circular cone is given by $A = \pi r \sqrt { r ^ { 2 } + h ^ { 2 } }$ , where r and h are the radius and height of the cone. Determine the exact value (in terms of ) of the lateral surface area of
A cone with radius 3 m and height 5 m. Then give a decimal approximation to the nearest square meter.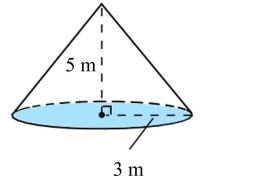

A) $6 \pi \sqrt { 2 } \mathrm {~m} ^ { 2 } \approx 27 \mathrm {~m} ^ { 2 }$
B) $10 \pi \sqrt { 2 } \mathrm {~m} ^ { 2 } \approx 44 \mathrm {~m} ^ { 2 }$
C) $5 \pi \sqrt { 34 } \mathrm {~m} ^ { 2 } \approx 92 \mathrm {~m} ^ { 2 }$
D) $3 \pi \sqrt { 34 } \mathrm {~m} ^ { 2 } \approx 55 \mathrm {~m} ^ { 2 }$