Multiple Choice
Graph the function.
-Use the graph of to obtain the graph of .
A) 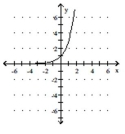
B) 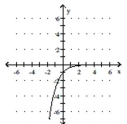
C) 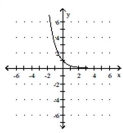
D) 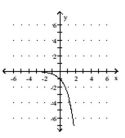
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q83: Find the domain of the logarithmic
Q84: Approximate the number using a calculator.
Q85: The graph of an exponential function
Q86: Graph the function.<br>- <span class="ql-formula" data-value="f(x)=\log
Q87: Approximate the number using a calculator.
Q88: Solve the problem.<br>-The function D(h) = 5e-0.4h
Q89: Use properties of logarithms to expand
Q91: The function f <span class="ql-formula"
Q92: Use properties of logarithms to expand
Q93: Use properties of logarithms to expand