Related Questions
Q239: Solve the equation exactly in the
Q240: <span class="ql-formula" data-value="\frac { 7 } {
Q241: Use the given graph of the polynomial
Q242: Provide an appropriate response.<br>-In the following
Q243: Use synthetic division to find the
Q245: Determine whether the polynomial function is cubic
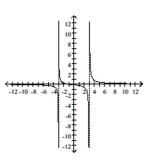
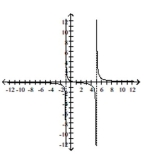
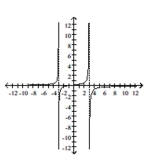
Q246: Give the equations of any vertical
Q247: Solve the polynomial equation by factoring.<br>-
Q248: Use analytical methods to solve the
Q249: Use the graph of the polynomial