Determine If the Function F Defined by the Arrow Diagram

Multiple Choice

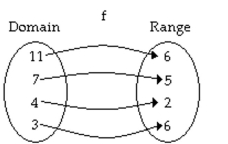
Determine if the function f defined by the arrow diagram has an inverse. If it does, create an arrow diagram that defines
the inverse. If not, explain why not.
-

A) Yes;
B) No; the function is not one-to-one