Multiple Choice
For the function as defined that is one-to-one, graph f and on the same axes.
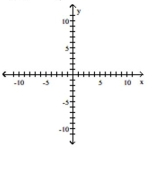
- 
A) 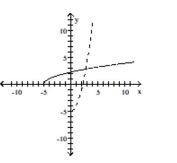
B) 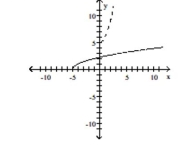
C) 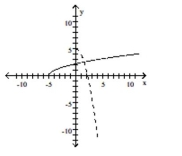
D) 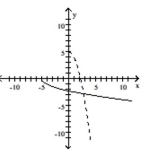
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q421: Use the change of base rule
Q422: Graph the function. Give the domain
Q423: Solve the equation.<br>- <span class="ql-formula" data-value="2401
Q424: Graph the function.<br>- <span class="ql-formula" data-value="f(x)=\left(\frac{2}{5}\right)^{x}"><span
Q425: Use properties of logarithms to evaluate
Q427: Choose the one alternative that best
Q428: Choose the one alternative that best
Q429: Write in logarithmic form.<br>- <span class="ql-formula"
Q430: Find the value. Give an approximation
Q431: The graph of a function f