Multiple Choice
For the function as defined that is one-to-one, graph f and on the same axes.
- 
A) 
B) Function is its own inverse
C) 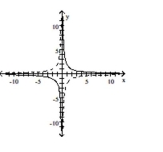
D) Function is its own inverse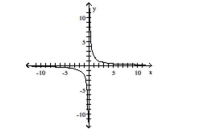
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q399: The graph of a function f
Q400: Solve for the indicated variable.<br>- <span
Q401: Determine whether or not the function
Q402: Find the present value of the future
Q403: Find the future value.<br>-$3742 invested for 12
Q405: Use the change of base rule
Q406: Determine whether or not the function
Q407: Write the word or phrase that
Q408: Solve for the indicated variable.<br>- <span
Q409: Given <span class="ql-formula" data-value="\log _