Multiple Choice
Graph the exponential function using transformations where appropriate.
- 
A) 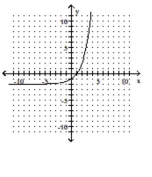
B) 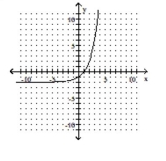
C) 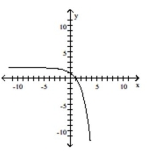
D) 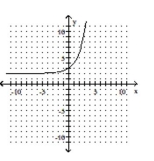
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q219: Find the domain and range of
Q220: Use the properties of logarithms to
Q221: An everyday activity is described. Keeping in
Q222: Explain how the graph of can
Q223: Write an equivalent expression in exponential
Q225: Choose the one alternative that best
Q226: Graph the function. Give the domain
Q227: Determine whether or not the function
Q228: Find the value. Give an approximation
Q229: For the function as defined that