Related Questions
Q267: Use the graph of f to sketch
Q268: Use properties of logarithms to evaluate
Q269: Choose the one alternative that best
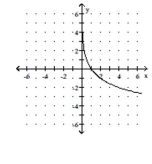
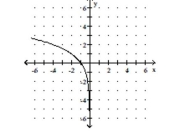
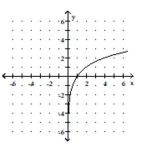
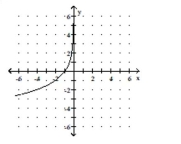
Q270: Match the function with its graph.<br>-
Q271: Solve the problem.<br>- <span class="ql-formula" data-value="\mathrm
Q273: Solve the equation and express the
Q274: Decide whether the given functions are
Q275: Use properties of logarithms to evaluate
Q276: Find the value. Give an approximation
Q277: Use properties of logarithms to evaluate