Multiple Choice
Sketch the graph of the rational function.
- 
A) 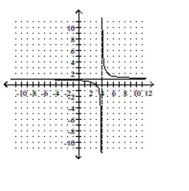
B) 
C) 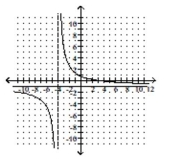
D) 
Correct Answer:

Verified
Correct Answer:
Verified
Related Questions
Q244: Find the equation of the axis
Q245: Determine which of the rational functions
Q246: Find all complex zeros of the
Q247: Give the equation of any oblique
Q248: Determine whether the statement is true or
Q250: Graph the polynomial function. Factor first
Q251: Translate the given formula to an
Q252: Find a polynomial function f(x) of
Q253: Graph the polynomial function. Factor first
Q254: Use a graphing calculator to find