Multiple Choice
Describe the transformations and give the equation for the graph.
-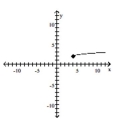
A) It is the graph of translated 4 units to the right, stretched vertically by a factor of 3 and translated 2 units up. The equation is
B) It is the graph of translated 4 units to the right, shrunken vertically by a factor of and translated 2 units up. The equation is
C) It is the graph of translated 4 units to the right, shrunken vertically by a factor of and translated 2 units up. The equation is
D) It is the graph of translated 4 units to the right, stretched vertically by a factor of 3 and translated 2 units up. The equation is
Correct Answer:

Verified
Correct Answer:
Verified
Q119: Find the center and radius of
Q120: Write all linear equations in slope-intercept form.<br>-A
Q121: Graph the point symmetric to the
Q122: The graph of y = f(x) is
Q123: Graph the linear function and give
Q125: The graph of a linear function
Q126: Determine whether the equation has a
Q127: Give the domain and range of
Q128: Give the domain and range of
Q129: Decide whether the relation defines a function.<br>-<img