Related Questions
Q77: Graph the curve whose parametric equations
Q78: Find the center, foci, and vertices
Q79: Rotate the axes so that the
Q80: Choose the one alternative that best
Q81: Solve the problem.<br>-An experimental model for a
Q83: Determine the appropriate rotation formulas to
Q84: Find parametric equations for the rectangular
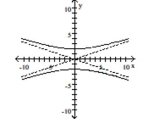
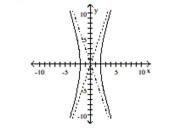
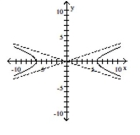
Q85: Match the equation to its graph.<br>-
Q86: Find a polar equation for the
Q87: Graph the curve whose parametric equations