Solve the Problem $( 0,4 )$ And Then Moves Closer and Closer to the Line

Multiple Choice

Solve the problem.
-A satellite following the hyperbolic path shown in the picture turns rapidly at $( 0,4 )$ and then moves closer and closer to the line $y = \frac { 8 } { 5 } x$ as it gets farther from the tracking station at the origin. Find the equation that describes the path of the rocket if the center of the hyperbola is at 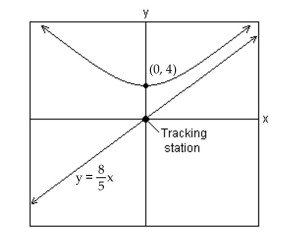$( 0,0 )$ .

A) $\frac { y ^ { 2 } } { \frac { 25 } { 4 } } - \frac { x ^ { 2 } } { 16 } = 1$
B) $\frac { x ^ { 2 } } { \left( \frac { 12 } { 5 } \right) ^ { 2 } } - \frac { y ^ { 2 } } { 9 } = 1$
C) $\frac { x ^ { 2 } } { 16 } - \frac { y ^ { 2 } } { \left( \frac { 16 } { 5 } \right) ^ { 2 } } = 1$
D) $\frac { y ^ { 2 } } { 16 } - \frac { x ^ { 2 } } { \frac { 25 } { 4 } } = 1$