Multiple Choice
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
- 
A) 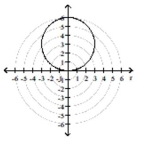
center at in rectangular coordinates
B) 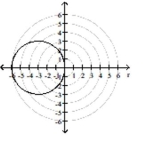
; circle, radius 3 center at in rectangular coordinates
C) 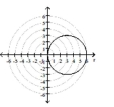
center at in rectangular coordinates
D) 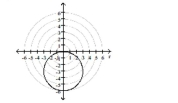
center at in rectangular coordinates
circle, radius 3 ; circle, radius 3 ,
center at in rectangular coordinates center at in rectangular coordinates
Correct Answer:

Verified
Correct Answer:
Verified
Q23: Plot the point given in polar
Q24: The vector v has initial position
Q25: Choose the one alternative that best
Q26: Write the complex number in rectangular
Q27: Test the equation for symmetry with
Q29: Solve the problem. Leave your answer
Q30: Find the indicated cross product.<br>- <span
Q31: Find the indicated cross product.<br>- <span
Q32: Find the angle between v and
Q33: Solve the problem. Leave your answer