Multiple Choice
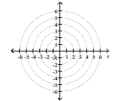
Transform the polar equation to an equation in rectangular coordinates. Then identify and graph the equation.
- 
A) 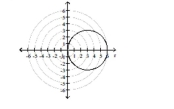
circle, radius 3 ,
center at in rectangular coordinates
B) 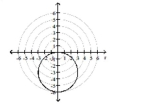
circle, radius 3,
center at in rectangular coordinates
C) 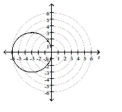
; circle, radius 3
center at in rectangular coordinates
D) 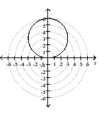
center at in rectangular coordinates
; circle, radius 3
center at in rectangular coordinates center at in rectangular coordinates
Correct Answer:

Verified
Correct Answer:
Verified
Q91: Find the quantity if v =
Q92: Find the area of the parallelogram
Q93: Solve the problem.<br>-If <span class="ql-formula"
Q94: Graph the polar equation.<br>- <span class="ql-formula"
Q95: Find the quantity if v =
Q97: Match the graph to one of
Q98: Graph the polar equation.<br>- <span class="ql-formula"
Q99: Write the expression in the standard
Q100: Choose the one alternative that best
Q101: Perform the indicated operation.<br>- <span class="ql-formula"