Multiple Choice
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
- 
A) domain of f: ; range of
horizontal asymptote: 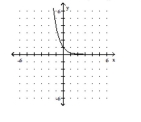
B) domain of ; range of ) horizontal asymptote: 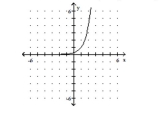
C) domain of ; range of
horizontal asymptote: 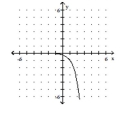
D) domain of ; range of horizontal asymptote: 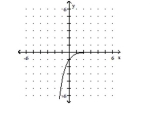
Correct Answer:

Verified
Correct Answer:
Verified
Q289: Choose the one alternative that best
Q290: Use transformations to graph the function.
Q291: Write the word or phrase that
Q292: Find a formula for the inverse
Q293: Choose the one alternative that best
Q295: Approximate the value using a calculator.
Q296: Choose the one alternative that best
Q297: Write the word or phrase that
Q298: Find the amount that results from
Q299: Use a graphing calculator to solve