Multiple Choice
Use transformations to graph the function. Determine the domain, range, and horizontal asymptote of the function.
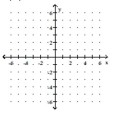
- 
A) domain of ; range of
horizontal asymptote: 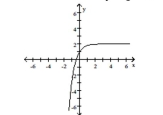
B) domain of ; range of horizontal asymptote: 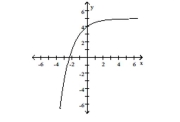
C) domain of ; range of
horizontal asymptote: 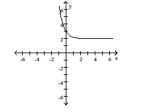
D) domain of ; range of horizontal asymptote: 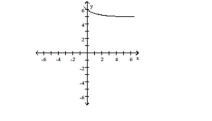
Correct Answer:

Verified
Correct Answer:
Verified
Q391: Choose the one alternative that best
Q392: Graph the function.<br>- <span class="ql-formula" data-value="\begin{array}{l}f
Q393: Choose the one alternative that best
Q394: Choose the one alternative that best
Q395: The function f is one-to-one. Find
Q397: Choose the one alternative that best
Q398: Choose the one alternative that best
Q399: Choose the one alternative that best
Q400: Write as the sum and/or difference
Q401: Choose the one alternative that best